http://infobiotics.org/

Table Of Contents

Previous topic

Structure and Parameter Optimization with poptimizer

Next topic

Pulse Generator

This Page

The Repressilator

Introduction

The Repressilator is one the first implemented synthetic genetic circuits. It was developed by Michael B. Elowitz and Stanislas Leibler [Elowitz2000] . It has been used as a canonical example in synthetic biology in various P system studies [Gheorghe2009].

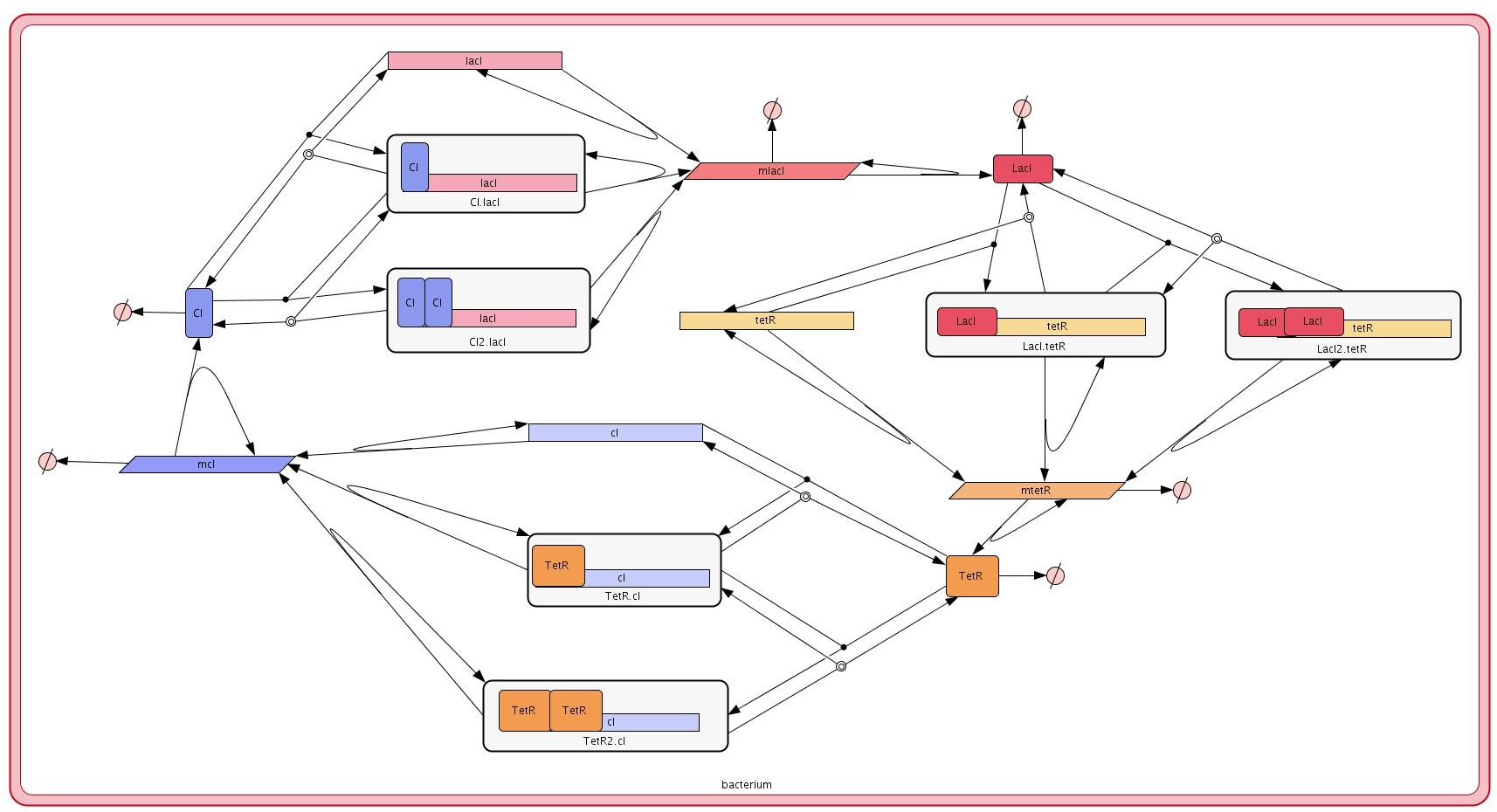
The Repressilator consists of three genes codifying three repressors. Namely, the operon lactose repressor, lacI, the repressor form the tetracycline transposon, tetR, and a repressor from the λ phage virus, cI. These genes are connected in a synthetic gene regulatory network such that LacI represses the expression of the tetR gene, which in turn represses the cI gene. Finally, the cycle is closed as CI represses the expression of the lacI gene.

alternate text

The complete model of the repressilator developed using Infobiotics workbench is available from this link.

The Model

Our model of the Repressilator consists of a single bacterial cell modelled as a SP-system identified with the name repressilatorCell. A bacterial colony of this cell type is then created by distributed cellular clones over the points of a rectangular lattice.

The molecular interactions in the corresponding SP-system are defined in a modular manner using the modules from the library basicLibrary below:

# Author: Francisco J. Romero-Campero                                                                #
# Date: 14 May 2010                                                                                                  #
# Description: A library containing basic gene regulatory            #
#                       mechanisms                                                                                   #

libraryOfModules basicLibrary

   # A module representing the unregulated expression of a gene X    #
   UnReg({X},{c_1, c_2, c_3, c_4},{l}) =
   {
      rules:
      # Transcription of geneX #
      r1: [ geneX ]_l -c_1-> [ geneX + rnaX ]_l
      # Degradation of the RNA #
      r2: [ rnaX ]_l -c_2-> [ ]_l
      # Translation of the RNA #
      r3: [ rnaX ]_l -c_3-> [ rnaX + proteinX ]_l
      # Degradation of the protein #
      r4: [ proteinX ]_l -c_4-> [ ]_l
   }

   # A module representing the positive regulation of a protein X #
   # over a gene Y                                                                                              #
   PosReg({X,Y},{c_1, c_2, c_3, c_4, c_5, c_6},{l}) =
   {
      rules:
      # Binding and debinding of the transcription factor proteinX to geneY #
      r1: [ proteinX + geneY ]_l -c_1-> [ proteinX_geneY ]_l
      r2: [ proteinX_geneY ]_l -c_2-> [ proteinX + geneY ]_l
      # Transcription of geneY when proteinX is bound to its promoter #
      r3: [ proteinX_geneY ]_l -c_3-> [ proteinX_geneY + rnaY ]_l
      # Degradation of the RNA #
      r4: [ rnaY ]_l -c_4-> [ ]_l
      # Translation of the RNA #
      r5: [ rnaY ]_l -c_5-> [ rnaY + proteinY ]_l
      # Degradation of the protein #
      r6: [ proteinY ]_l -c_6-> [ ]_l
   }

   # A module representing the negative regulation of a protein X    #
   # over a gene Y                                                                                                   #
   NegReg({X,Y},{c_1, c_2},{l}) =
   {
      rules:
      # Binding and debinding of the transcription factor proteinX to gene Y #
      r1: [ proteinX + geneY ]_l -c_1-> [ proteinX_geneY ]_l
      r2: [ proteinX_geneY ]_l -c_2-> [ proteinX + geneY ]_l
   }

   # A module representing the cooperative regulation of a protein#
   # X over a gene Y #
   CoopNegReg({X,Y},{c_1, c_2, c_3, c_4, c_5, c_6},{l}) =
   {
      rules:
      r1: [ proteinX + geneY ]_l -c_1-> [ proteinX_geneY ]_l
      r2: [ proteinX_geneY ]_l -c_2-> [ proteinX + geneY ]_l
      r3: [ proteinX + proteinX_geneY ]_l -c_3-> [ proteinX2_geneY ]_l
      r4: [ proteinX2_geneY ]_l -c_4-> [ proteinX + proteinX_geneY ]_l
      r5: [ proteinX_geneY ]_l -c_5-> [ proteinX_geneY + rnaY ]_l
      r6: [ proteinX2_geneY ]_l -c_6-> [ proteinX2_geneY + rnaY ]_l
   }

endLibraryOfModules

The cell type or bacterial strain carrying the repressilator is modelled using the following SP-system:

# Author: Francisco J. Romero-Campero #
# Date: 14 May 2010  #
# Description: A single cell carrying the repressilator #
SPsystem repressilatorCell

   # Molecular species present in the system #
   alphabet
      geneCI
      geneLacI
      geneTetR
      proteinCI
      proteinCI2_geneLacI
      proteinCI_geneLacI
      proteinLacI
      proteinLacI2_geneTetR
      proteinLacI_geneTetR
      proteinTetR
      proteinTetR2_geneCI
      proteinTetR_geneCI
      rnaCI
      rnaLacI
      rnaTetR
   endAlphabet

   # This model consists of a single compartment #
   compartments
      bacterium
   endCompartments

   # In the initial state of the system only a single copy of the #
   # genes lacI, cI and tetR are present #
   initialMultisets
      initialMultiset bacterium
         geneLacI     1
         geneCI       1
         geneTetR     1
      endInitialMultiset
   endInitialMultisets

   # The molecular interactions involved in the reprissilator #
   ruleSets
      ruleSet bacterium

         # CI represses cooperatively the lacI gene which expressed constitutively otherwise #
         CoopNegReg({CI,LacI},{1,224,1,9,0.0005,0.0005},{bacterium}) from basicLibrary.plb
         UnReg({LacI},{0.5,0.00578,0.167,0.00116},{bacterium}) from basicLibrary.plb

         # LacI represses cooperatively the tetR gene which expressed constitutively otherwise #
         CoopNegReg({LacI,TetR},{1,224,1,9,0.0005,0.0005},{bacterium}) from basicLibrary.plb
         UnReg({TetR},{0.5,0.00578,0.167,0.00116},{bacterium}) from basicLibrary.plb

         # TetR represses cooperatively the cI gene which expressed constitutively otherwise #
         CoopNegReg({TetR,CI},{1,224,1,9,0.0005,0.0005},{bacterium}) from basicLibrary.plb
         UnReg({CI},{0.5,0.00578,0.167,0.00116},{bact}) from basicLibrary.plb

      endRuleSet
   endRuleSets
endSPsystem

The geometry of a bacterial colony of the cell type or bacterial strain represented in the previous model is captured using the following rectangular lattice:

# Author: Francisco J. Romero-Campero              #
# Date: July 2010                                  #
# Description: A rectangular lattice of size 5x5 #

lattice rectangularLattice

   # Dimension of the lattice and lower/upper bounds #
   dimension 2
   xmin      0
   xmax      4
   ymin      0
   ymax      4

   # Parameters used in the definition of the rest of components defining the lattice #
   parameters
      parameter b1 value = 2
      parameter b2 value = 1
   endParameters

   # Basis vector determining the points in the lattice #
   # in this case we have a rectangular lattice         #
   basis
      (b1,0)
      (0,b2)
   endBasis

   # Vertices used to determine the shape of the outmost membrane #
   # of the SP systems located on each point of the lattice       #
   vertices
      (b1/2,b2/2)
      (-b1/2,b2/2)
      (-b1/2,-b2/2)
      (b1/2,-b2/2)
   endVertices

   # Vectors pointing at the neighbours of each point of the lattice #
   neighbours
      (1,0)    (1,1)    (0,1)   (-1,1)
      (-1,0)   (-1,-1)  (0,-1)  (1,-1)
   endNeighbours

endLattice

Finally, the model of a bacterial colony is obtained by distributing cellular clones of the bacterial cell carrying the repressilator over the points of the previous lattice. This is modelled using the LPP-system below:

# Author: Francisco J. Romero-Campero #
# Date: July 2010 #
# Description: A multicelluar system consisting of a bacterial colony #
#              carrying the repressilator #

LPPsystem repressilatorColony

   # Cell types specified as individual SP systems #
   SPsystems
      SPsystem repressilator from repressilator.sps
   endSPsystems

   # The geometry of the system is determine using a regular finite point lattice #
   lattice rectangular from rectangular.lat

   # Spatial distribution of the cells over the lattice #
   spatialDistribution

      # Bacteria carrying the repressilator are distributed over all the points of the lattice #
      positions for repressilator
        parameters
           parameter i = 0:1:4
           parameter j = 0:1:4
        endParameters
        coordinates
           x = i
           y = j
        endCoordinates
      endPositions

   endSpatialDistribution
endLPPsystem

The complete model of the repressilator developed using the Infobiotics workbench can be download from this link.

Simulations

Stochastic simulations of our model of the repressilator can be run using the Infobiotics workbench. For this, please load using the provided interface the simulation parameter file, simulation_paramters.params, provided with the files comprising this example. Be patient, these simulations could take a few minutes.

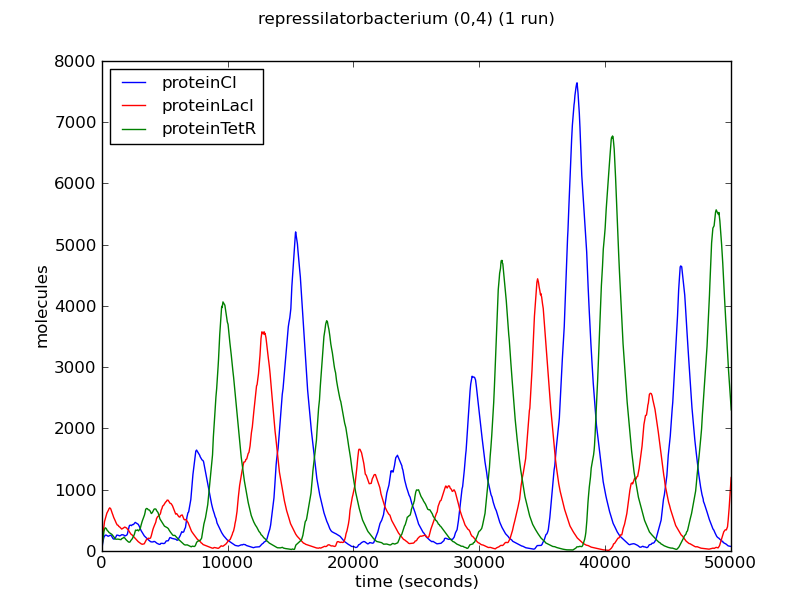
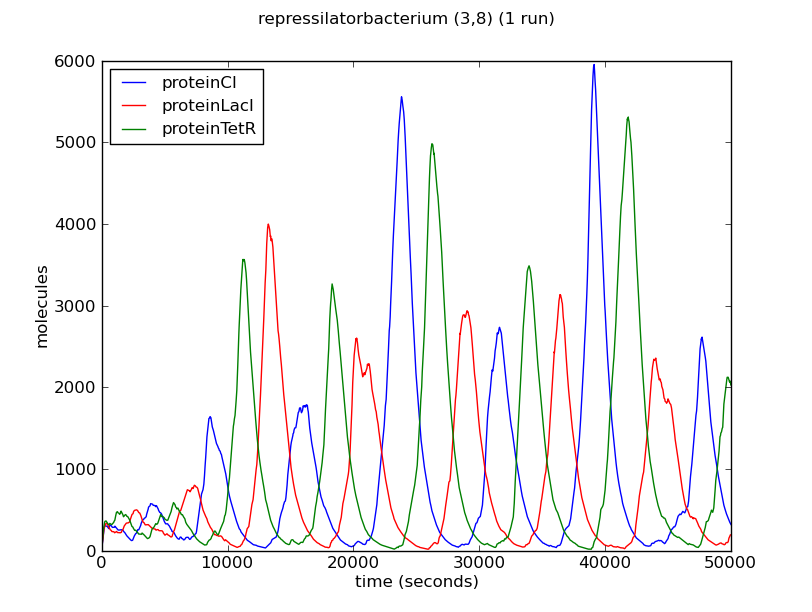
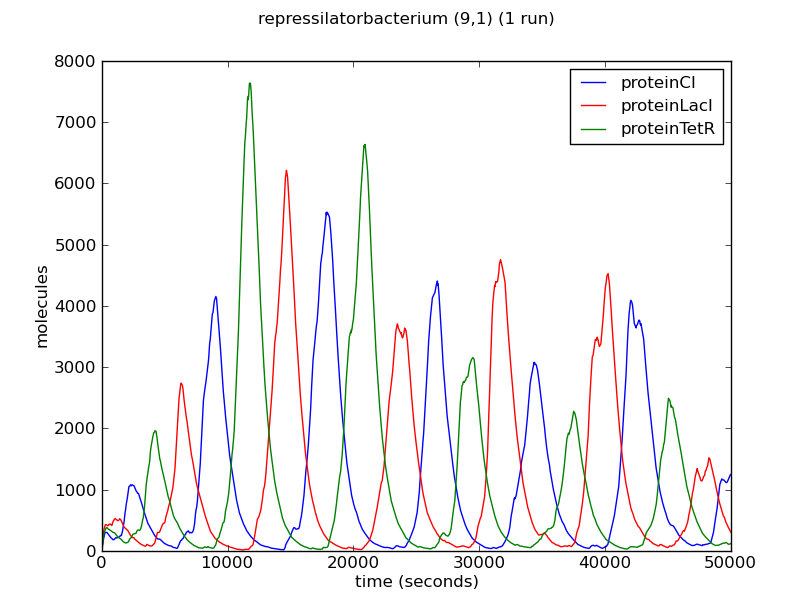
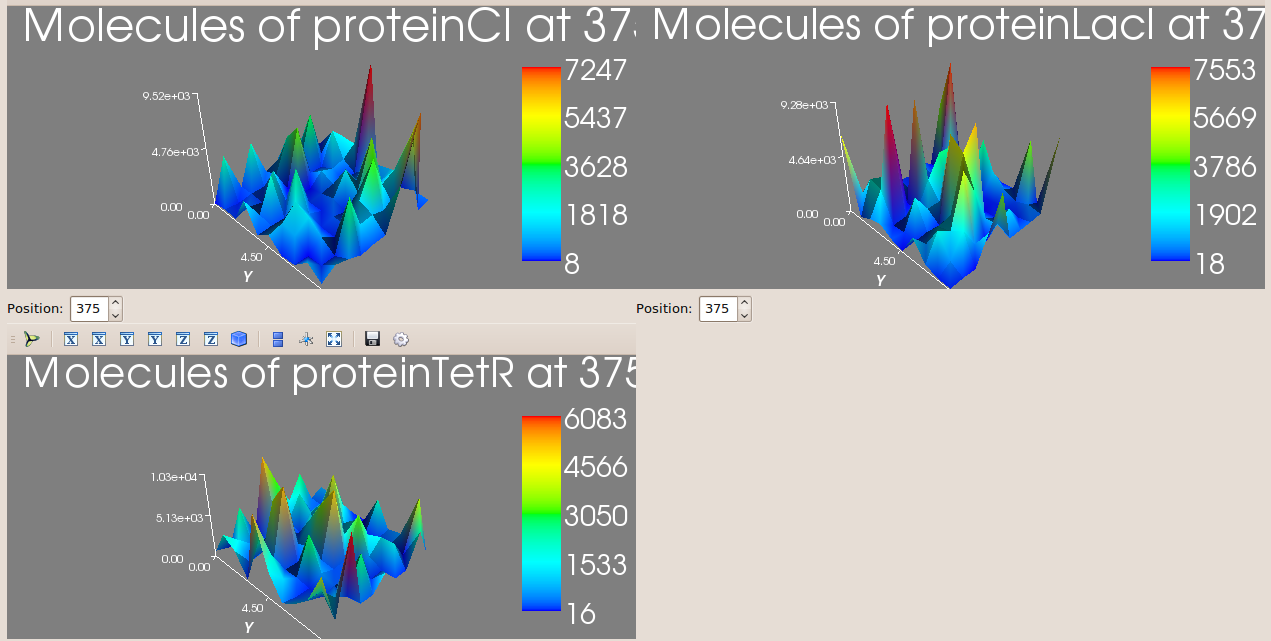
Below we show the evolution over time of the number of proteins LacI, CI and TetR in three different bacteria from the colony. Note that the system exhibits oscillatory behaviour that is not synchronised between different bacteria.

alternate text
alternate text
alternate text

The oscillatory behaviour of the system and the lack of synchronisation between bacteria can be observed more clearly in the dynamics of the entire colony:

alternate text

This video shows the spatio-temporal evolution of the number of proteins LacI, CI and TetR in our model of a bacterial colony carrying the repressilator.

Model Checking

Model checking of some stochastic properties of the repressilator were run using the Infobiotics workbench. For this, please load using the provided interface the model checking parameter file, model_checking_mc2.params, provided with the files comprising this example. Be patient, this analysis could take a few minutes.

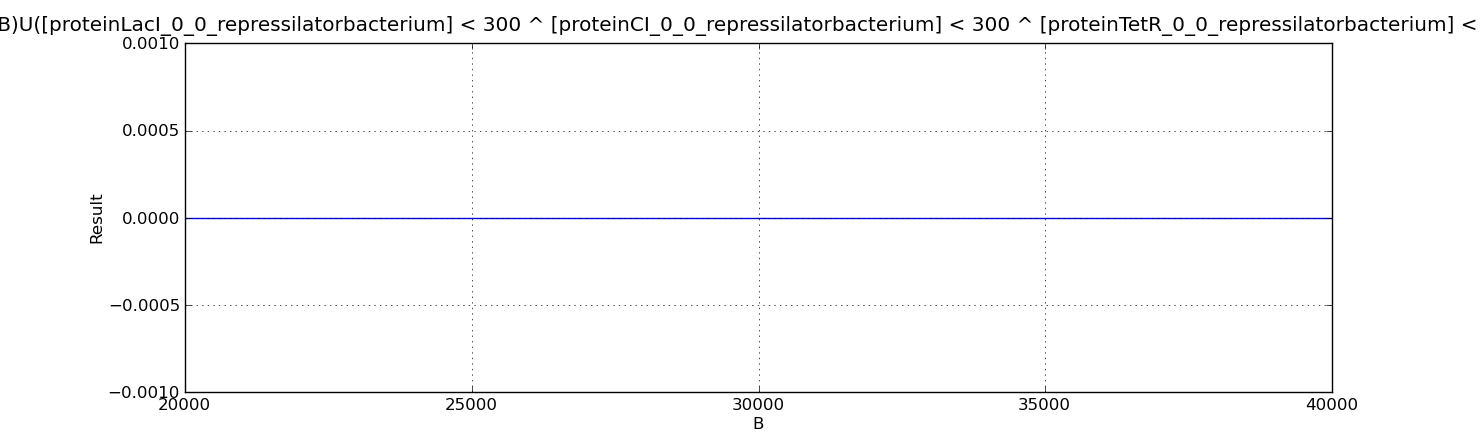
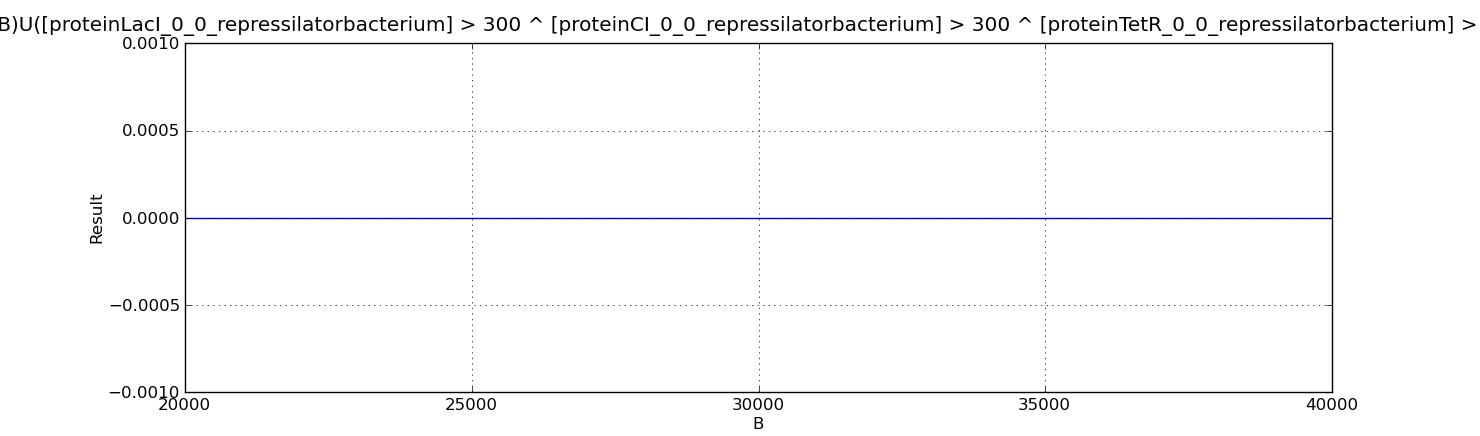
Below we show the analysed properties. They are used to compute the probability of having more or fewer than 300 proteins of LacI, CI and TetR simultaneously over different time points of the evolution.
P=?[ (Time=B)U([proteinLacI_0_0_repressilatorbacterium] > 300 ^ [proteinCI_0_0_repressilatorbacterium] > 300 ^ [proteinTetR_0_0_repressilatorbacterium] > 300 ){Time=B}]

P=?[ (Time=B)U([proteinLacI_0_0_repressilatorbacterium] < 300 ^ [proteinCI_0_0_repressilatorbacterium] < 300 ^ [proteinTetR_0_0_repressilatorbacterium] < 300 ){Time=B}]

Below we present the results for the properties above. In both cases the probability is zero which suggests that the three proteins simultaneously cannot be above or below 300 molecules, they should be alternatively oscillating.

alternate text
alternate text
http://infobiotics.org/
© Copyright 2010, Infobiotics Project. Created using Sphinx 0.6.2.